whats it mean for a problem to be np hard

Complication class

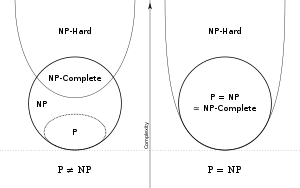
Euler diagram for P, NP, NP-complete, and NP-hard prepare of problems. The left side is valid under the assumption that P≠NP, while the right side is valid nether the supposition that P=NP (except that the empty language and its complement are never NP-complete)

In computational complication theory, NP-hardness (non-deterministic polynomial-fourth dimension hardness) is the defining property of a grade of bug that are informally "at least as hard equally the hardest issues in NP". A simple example of an NP-hard problem is the subset sum problem.

A more than precise specification is: a problem H is NP-hard when every problem Fifty in NP can be reduced in polynomial time to H; that is, assuming a solution for H takes i unit time, H‎'s solution can be used to solve L in polynomial time.^{[one] [ii]} As a consequence, finding a polynomial time algorithm to solve any NP-hard problem would requite polynomial time algorithms for all the bug in NP. As it is suspected that P≠NP, information technology is unlikely that such an algorithm exists.^[3]

A common misconception is that the NP in "NP-hard" stands for "not-polynomial" when in fact it stands for "non-deterministic polynomial acceptable bug".^[four] Information technology is suspected that at that place are no polynomial-time algorithms for NP-hard problems, only that has not been proven.^[5] Moreover, the class P, in which all problems can be solved in polynomial fourth dimension, is independent in the NP class.^{[half dozen]}

Definition [edit]

A decision problem H is NP-difficult when for every problem L in NP, there is a polynomial-time many-ane reduction from L to H.^{[1] : eighty} An equivalent definition is to require that every trouble L in NP can be solved in polynomial fourth dimension by an oracle automobile with an oracle for H.^[7] Informally, an algorithm tin be thought of that calls such an oracle machine as a subroutine for solving H and solves L in polynomial time if the subroutine phone call takes but one step to compute.

Some other definition is to require that there be a polynomial-time reduction from an NP-complete trouble G to H.^{[1] : 91} As whatever problem L in NP reduces in polynomial time to G, Fifty reduces in plough to H in polynomial fourth dimension so this new definition implies the previous 1. Awkwardly, it does not restrict the form NP-hard to determination issues, and information technology too includes search problems or optimization bug.

Consequences [edit]

If P ≠ NP, then NP-difficult issues could not be solved in polynomial time.

Some NP-hard optimization problems can be polynomial-time approximated up to some constant approximation ratio (in detail, those in APX) or even up to any approximation ratio (those in PTAS or FPTAS).

Examples [edit]

An case of an NP-hard trouble is the decision subset sum problem: given a prepare of integers, does any not-empty subset of them add up to nada? That is a decision problem and happens to be NP-complete. Some other example of an NP-hard problem is the optimization problem of finding the least-cost circadian route through all nodes of a weighted graph. This is commonly known as the travelling salesman problem.^[eight]

There are decision problems that are NP-difficult but not NP-complete such every bit the halting problem. That is the problem which asks "given a program and its input, will it run forever?" That is a yep/no question and then is a decision problem. It is piece of cake to prove that the halting problem is NP-difficult but not NP-complete. For example, the Boolean satisfiability problem can be reduced to the halting trouble by transforming information technology to the clarification of a Turing machine that tries all truth value assignments and when information technology finds one that satisfies the formula it halts and otherwise it goes into an infinite loop. It is too like shooting fish in a barrel to see that the halting trouble is non in NP since all problems in NP are decidable in a finite number of operations, but the halting problem, in general, is undecidable. In that location are too NP-hard issues that are neither NP-complete nor Undecidable. For instance, the linguistic communication of true quantified Boolean formulas is decidable in polynomial space, but not in not-deterministic polynomial fourth dimension (unless NP = PSPACE).^[9]

NP-naming convention [edit]

NP-difficult problems do not have to be elements of the complexity class NP. As NP plays a central part in computational complexity, it is used as the footing of several classes:

NP

Class of computational decision problems for which any given yes-solution can exist verified as a solution in polynomial time by a deterministic Turing car (or solvable by a non-deterministic Turing automobile in polynomial fourth dimension).

NP-difficult

Class of problems which are at least as hard every bit the hardest problems in NP. Problems that are NP-hard do non have to be elements of NP; indeed, they may not even be decidable.

NP-complete

Class of determination problems which contains the hardest problems in NP. Each NP-complete problem has to be in NP.

NP-easy

At well-nigh as hard as NP, merely not necessarily in NP.

NP-equivalent

Decision problems that are both NP-hard and NP-piece of cake, but not necessarily in NP.

NP-intermediate

If P and NP are different, then there exist decision problems in the region of NP that fall between P and the NP-consummate problems. (If P and NP are the same course, then NP-intermediate problems do non exist considering in this case every NP-complete problem would autumn in P, and by definition, every problem in NP tin be reduced to an NP-complete problem.)

Application areas [edit]

NP-hard problems are ofttimes tackled with rules-based languages in areas including:

• Guess calculating
• Configuration
• Cryptography
• Information mining
• Decision support
• Phylogenetics
• Planning
• Process monitoring and command
• Rosters or schedules
• Routing/vehicle routing
• Scheduling

References [edit]

1. ^ ^{a b c} Leeuwen, Jan van, ed. (1998). Handbook of Theoretical Information science. Vol. A, Algorithms and complication. Amsterdam: Elsevier. ISBN0262720140. OCLC 247934368.
2. ^ Knuth, Donald (1974). "Postscript about NP-hard problems". ACM SIGACT News. half dozen (two): fifteen–16. doi:10.1145/1008304.1008305. S2CID 46480926.
3. ^ Daniel Pierre Bovet; Pierluigi Crescenzi (1994). Introduction to the Theory of Complexity. Prentice Hall. p. 69. ISBN0-xiii-915380-2.
4. ^ "P and NP". www.cs.uky.edu. Archived from the original on 2016-09-19. Retrieved 2016-09-25 .
5. ^ "Shtetl-Optimized » Blog Archive » The Scientific Case for P≠NP". www.scottaaronson.com . Retrieved 2016-09-25 .
6. ^ "PHYS771 Lecture 6: P, NP, and Friends". www.scottaaronson.com . Retrieved 2016-09-25 .
7. ^ 5. J. Rayward-Smith (1986). A First Course in Computability. Blackwell. p. 159. ISBN0-632-01307-9.
8. ^ Lawler, E. L.; Lenstra, J. K.; Rinnooy Kan, A. H. G.; Shmoys, D. B. (1985), The Traveling Salesman Problem: A Guided Bout of Combinatorial Optimization , John Wiley & Sons, ISBN0-471-90413-9 .
9. ^ More precisely, this language is PSPACE-consummate; see, for example, Wegener, Ingo (2005), Complexity Theory: Exploring the Limits of Efficient Algorithms, Springer, p. 189, ISBN9783540210450 .

• Michael R. Garey and David South. Johnson (1979). Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman. ISBN0-7167-1045-five.

jenningsknours.blogspot.com

Source: https://en.wikipedia.org/wiki/NP-hardness

Share this post